Metainformationen zur Seite
Kartennetzentwürfe, Geodätisches Datum und Projektionen
Im Kontext von GIS bezieht sich der Begriff „Raum“ auf Orte, Flächen oder Strecken auf der gekrümmten und unregelmäßig geformten Erdoberfläche, die nicht exakt geometrisch sind. Um diese raumbezogenen Daten auf eine exakt geometrische Form wie zum Beispiel eine rechteckige Fläche (z.B. Karte, Bildschirm) zu projizieren, müssen wir die Erde idealisieren. Um die Positionen von Orten genau bestimmen zu können, benötigen wir ein Netz-System, das als Koordinatensystem oder Kartennetzentwurf bekannt ist. Auf diese Weise wird das Ziel erreicht, „das Runde in das Eckige“ zu bringen und unsere raumbezogenen Daten in einer für uns verständlichen und nutzbaren Weise darzustellen.
Kartenprojektionen und Kartennetzentwurf
Die Verebnung der dreidimensionalen Erdgestalt auf eine Fläche verstehen wir als Projektion. Als würde man in einem Globus eine (starke) Lichtquelle installieren und in einem dunklen Raum einschalten: Die Kontinente auf dem Globus werden auf die Wände projiziert - verzerrt und falsch in ihrer Fläche, Winkel oder Länge (Verzerrungseigenschaften). Da diese Methode der Projektion nur bedingt zu dem erwünschten Ergebnis führt, gibt es genauere, geometrisch-mathematisch berechnete Projektions-Ideen.
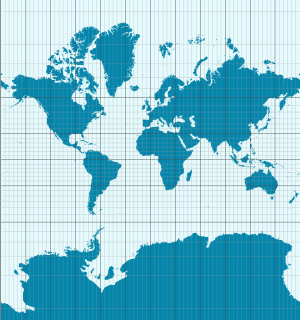
1569 ist es dem genialen Kartografen und Geografen Gerhard Mercator (Abb. 1) erstmals gelungen, die gesamte Erde auf eine Fläche zu projizieren (Mercator Projektion - Abb. 2) und revolutionierte damit die Navigation und Ortsbestimmung von Schiffen und der Kartografie allgemein. Er bedient sich dabei eines gedachten Zylinders (Hilfsfläche), welchen er über die Erde stülpt und diese am Äquator berührt. Projiziert man nun vom Erdinneren heraus die Erdoberfläche auf den Zylinder und schneidet diesen auf, erhält man eine flächige Erdabbildung (Zylinderabbildung). Weiter war es nun möglich diese verebnete Erde mit einem relativ simplen kartesischen Koordinatensystem zu überziehen - es entstand der erste globale Kartennetzentwurf mit Äquator und Nullmeridian.
Seit an wurden immer weiter Modelle entwickelt - es gibt inzwischen hunderte - welche alle für einen bestimmten Zweck maximal geeignet sind. Aber keines davon ist wirklich exakt, denn mathematisch betrachtet ist es unmöglich einen 3-Dimensionalen Körper verzerrungsfrei auf eine Fläche zu bringen. Wie wir auch vorgehen, das einzige was wir tun können ist die für unsere Aufgabenstellung richtige Auswahl zu treffen.
In Deutschland verwenden wir beispielsweise seit 1995 das Universal Transvers Mercartor System (UTM, auf Grundlage der transversalen Mercator-Projektion in Kombination mit einem kartesischen Koordinatensystem) in den Zonen 32 und 33 Nord. Vorher kam das Gauß-Krüger-Koordinatensystem mit seinen 3 bzw. 6 über Deutschland verteilten Zonen zum Einsatz. Da die Umstellung nicht sonderlich weit zurück liegt, werden wir immer wieder mit beiden Systemen konfrontiert was nicht selten zu, mitunter erheblichen, Problemen führt!
Nicht verstanden? Kein Problem, die Sendung mit der Maus erklärt es verständlicher! Teil 1: https://youtu.be/XRBzNZYiZRQ und Teil 2: https://youtu.be/0EKF8_5dnMk
Spannde Links zum Ausprobieren: Die wahre Größe der Länder
Das Geoid und das Geodätische Datum
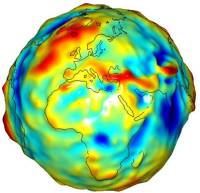
Das Problem der Erdprojektion ist jedoch nicht das einzige denn die Erde ist nicht perfekt rund und homogen, wie wir es uns gerne vorstellen. Gebirge, Ebenen und Ozeanböden haben alle eine unterschiedliche Dichte und folglich eine unterschiedlich starke Gravitation, was sich u.A. auch auf den Meeresspiegel auswirkt. Wenn wir von der Erdgestalt in ihrer tatsächlichen, physikalischen Ausprägung sprechen, verwenden wir hierfür den Begriff Geoid (Abb. 3).
Definition „Geoid“ nach Resnik, B. und Bill, R., 2009: Niveaufläche des von verschiedenen Einflüssen (z.B. Erdgezeiten, Luftdruckschwankungen) befreiten Erdschwerefeldes in Höhe des mittleren Meeresniveaus. Gedanklich definiert durch mittleren Meeresspiegel und dessen imaginärer Weiterführung unter den Kontinenten. Physikalisches Modell der Erdfigur, entwickelt von Gauß und Listing im 19. Jahrhundert, im Unterschied zu den mathematisch-geometrischen Modellen Ellipsoid und Kugel. Höhen- und Schwereangaben beziehen sich i.d.R. auf das Geoid. Die Abweichungen des Geoides von einem Referenzellipsoid betragen maximal um etwa 100 m.
Die Höhen und Tiefen unserer Erdoberfläche bewegen sich zwischen -420m (totes Meer) und 8848m (Mt. Everest)… aber wie können wir eine solche Aussage treffen? Von welcher Höhe gehen wir denn aus? Was ist dieses „Normal Null“? Eine Nullhöhe benötigen wir ja, um etwa eine Aussage treffen zu können wie: „Die Zugspitze ist mit 2962m der höchste Berg Deutschlands.“!
Hierfür bedienen wir uns einem idealisierten Körper, dem Referenzellipsoid (Abb. 4) welches an tausenden von Festpunkten auf der Erde verankert ist. Nun könnte uns das genügen, jedoch gibt es hierfür wieder mehrere Ansätze und entsprechend viele historisch gewachsene unterschiedliche Modelle (GRS80, ETRS89, WGS84, RD83, ED50 und ED79…). Mit dem Einsatz von Satelliten waren wir erstmals in der Lage Positionsangaben nicht lagebezogen auf einen Ort auf der Erde zu ermitteln, sondern quasi aus der Luft heraus. Es folgte das World Geodedic System 84 (WGS84) welches an 12 globalen Fundamentalstationen verankert ist und heute als „quasi-Standard“ der GPS-Navigation und Geoinformationssysteme zählt.
In Europa (und damit auch in Deutschland) verwenden wir das Europäische Terrestrische Referenzsystem (ETRS) bzw. das Internationale Terrestrische Referenzsystem (ITRS). Es ist für Europa das geeignetere Bezugsystem für präzise Messungen und Planungen, wobei der Genauigkeits-Unterschied zu WGS84 mit wenigen Zentimetern minimal ausfällt.
Koordinatenreferenzsystem/Koordinatenbezugssystem (KRS/KBS)
Das Koordinatenreferenzsystem bzw. das Koordinatenbezugssystem definiert des Geodätische Datum, die Projektion sowie das Koordinatensystem.
Es ist quasi die Maßeinheit - nur damit kann ein Koordinatendupel eindeutig einem Ort zugeordnet werden. Was für einen Preis/Wert in einem Land die Währung ist, ist für Koordinatenpaare das KBS. Oder anders: „Heute ist es 30… warm!“ ist das warm oder kalt? Die Einheit macht's: Fahrenheit oder Grad Celsius? Die Zahl 30 allein hat keine Aussagekraft für uns ohne dass wir die Einheit kennen…
EPSG (European Petroleum Survey Group)
Was hat Öl und Gas mit Koordinaten zu tun? An sich nichts! Aber die European Petroleum Survey Group hat den EPSG-Code ins Leben gerufen: eine eindeutige ID (SRID) zur Identifikation verschiedener Koordinatenbezugssysteme anhand einer 4 bis 5-stelligen Schlüsselnummer welche in einer offenen Datenbank beschrieben sind. Damit wurde die Identifikation der mit unter komplex beschriebenen KBS's auf eine maximal 5-stellige Ziffer reduziert und erheblich vereinfacht. Die meisten GIS-Systeme verstehen diese EPSG-Codes.
Auf der Seite http://epsg.io/ kann man nicht nur sehen, was sich hinter einem EPSG-Code verbirgt, sondern auch den richten EPSG-Code für ein neues Projekt ausfindig machen!
Beispiele:
| EPSG-Code | Koordinatenreferenzsystem | Bemerkung |
|---|---|---|
| 4326 | WGS-84 / geographisch 2D | weltweites System für GPS-Geräte, OpenStreetMap Datenbank |
| 25832 | ETRS89 / UTM Zone 32N | von 6° O bis 12° O - Fläche: Deutschland (West+Mitte) + Österreich (West) + Schweiz |
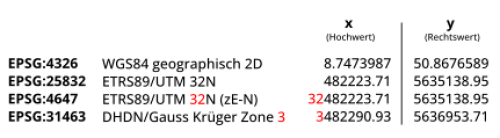
| 4647 | ETRS89 / UTM Zone 32N (zE-N) | Das Gleiche wie 25832 mit vorangestellter Zonen-Nummer an den Koordinaten |
| 25833 | ETRS89 / UTM Zone 33N | von 12° O bis 18° O - Fläche: Deutschland (Ost) + Österreich (Mitte+Ost) |
| 5650 | ETRS89 / UTM Zone 33N (zE-N) | Das Gleiche wie 25833 mit vorangestellter Zonen-Nummer an den Koordinaten |
| 31466 | DHDN / Gauß-Krüger Zone 2 | Fläche: Deutschland - westlich von 7,5° O |
| 31467 | DHDN / Gauß-Krüger Zone 3 | Fläche: Deutschland - von 7,5° O bis 10,5° O |
| 31468 | DHDN / Gauß-Krüger Zone 4 | Fläche: Deutschland - von 10,5° O bis 13,5° O |
| 31469 | DHDN / Gauß-Krüger Zone 5 | Fläche: Deutschland - von 13,5° O bis 16,5° O |
| 3857 | WGS 84 / Pseudo-Mercator | Google Maps, OpenStreetMap und andere Kartenanbieter im Netz. |
Messungen: Planimetrisch versus Ellipsoidal
Eine immer wieder aufkommende Frage ist: Warum erhalte ich unterschiedliche Messergebnisse? Das liegt daran, dass es unterschiedliche Methoden zur Berechnung von Flächen, Winkeln und Längen gibt. Das ist abhängig davon, ob ich auf der dreidimensionalen Erdoberfläche messe, oder auf der verebneten Karte.
Planimetrische Messung
Bei dieser Methode wird die Fläche direkt auf der Karte gemessen, ohne Berücksichtigung der Erddrehung, also ohne Berücksichtigung der Höhe der Erdoberfläche. Planimetrische Messungen sind am besten geeignet, wenn die Unterschiede zwischen den Koordinatenbezugssystemen vernachlässigt werden können oder wenn nur kleine Flächen gemessen werden.
Ellipsodiale Messung
Bei dieser Methode wird die Fläche unter Berücksichtigung der Krümmung der Erdoberfläche und der Abflachung des Ellipsoids, auf der das Koordinatensystem basiert, berechnet. Es berücksichtigt die Distanz zwischen den Koordinaten, die Höhe über dem Ellipsoid und die Krümmung des Ellipsoiden. Ellipsoidale Messungen sind am besten geeignet, wenn eine hohe Genauigkeit erforderlich ist oder wenn die zu messende Fläche groß ist.
area($geometry) gibt die planimetrische Fläche der Geometrie im Einheitensystem des Koordinatenbezugssystems zurück. Das bedeutet, dass die Fläche direkt auf der Karte gemessen wird, ohne Berücksichtigung der Erddimensionen.
$area gibt die ellipsodiale Fläche der Geometrie unter Berücksichtigung der Krümmung der Erdoberfläche und der Abflachung des Ellipsoids zurück. Die Fläche wird in Quadratmetern (oder Quadratfuß, etc.) berechnet, abhängig vom Einheitensystem des Koordinatenbezugssystems. Diese Funktion führt eine ellipsoidale Messung durch und ist daher genauer als die area($geometry)-Funktion.
Und was verwende ich nun zum Berechnen von Flächen - ellipsodial oder planimetrisch?
ChatGPT dazu:
„Ellipsoidale Flächenberechnung bezieht sich auf Methoden, die die Erdkrümmung berücksichtigen, indem sie das Ellipsoidmodell der Erde verwenden. Diese Methode ist für großräumige Berechnungen über lange Distanzen genauer, insbesondere wenn es um Gebiete geht, die sich über mehrere Längen- und Breitengrade erstrecken. Sie ist komplexer und rechenintensiver, bietet aber eine höhere Genauigkeit für großflächige Karten.
Planimetrische Flächenberechnung hingegen behandelt die Erdoberfläche als eine ebene Fläche und ignoriert die Erdkrümmung. Diese Methode ist einfacher und weniger rechenintensiv, kann jedoch bei großen Flächen oder bei Berechnungen, die sich über große geographische Distanzen erstrecken, zu Ungenauigkeiten führen. Für lokale oder kleinräumige Karten, wo die Krümmung der Erde eine vernachlässigbare Rolle spielt, ist die planimetrische Methode oft ausreichend.
“ - dem hab ich nichts hinzu zu fügen